Sound

The Physics of Sound

Definition: Sound

Sound is what our brains perceive when our ears detect variations in the pressure of the air surrounding us.

When air pressure at a given point in space is high, the air particles around that point are more tightly packed and moving with a greater speed. If you were to place something at a point with high air pressure, it would experience greater forces from the air surrounding it. Conversely, when air pressure is low, air particles are sparsely distributed and are moving with a lower speed. If you were to place something at a point with low air pressure, it would experience less force from the air surrounding it.

As air pressure near our ears changes, the forces exerted by the air particles on our ears cause some parts of the inside of the ears to move. These movements are then turned into electric signals by special cells in the ear and subsequently propagate through the neurons inside the brain to be ultimately interpreted as sound.

Tip: Sound

Sound is a subjective experience of an objective physical phenomenon.

How do we know that it is the changes which matter and not the pressure itself? Well, if this were not the case, then listening to a song at home would sound completely different from listening to the same song on a mountain peak, since the overall pressure of the air at the top of the mountain is less than the overall pressure of the air in your living room. However, we do not experience any significant difference in practice, indicating that our ears are primarily designed to detect pressure changes and not absolute pressure.

Waveforms

Definition: Waveform

The waveform of a sound is a graph which illustrates how air pressure varies in time as the sound is playing.

The horizontal axis represents time and the vertical axis shows something called amplitude. The details of what amplitude actually is are largely irrelevant to music production and are related to how digital and analog audio signals are recorded and converted into one another. The important thing is that amplitude has one crucial property - it is directly proportional to changes in air pressure. This means that the shape of the amplitude’s graph is the same as the shape of the graph of the air pressure.

An amplitude of $0.0$ is assigned to atmospheric pressure, i.e. the air pressure when no sound is playing. The choice of what pressure corresponds to an amplitude of $-1.0$ and what pressure corresponds to an amplitude of $1.0$ is rather arbitrary. What matters is that pressure values below atmospheric pressure are assigned negative amplitudes and pressure values above atmospheric pressure are assigned higher amplitudes, making visualization more intuitive.

One convention is to assign an amplitude of $-1.0$ to the lowest value to which air pressure drops while the sound is playing and an amplitude of $1.0$ to the highest value to which air pressure rises while the sound is playing. This is a common thing to do when analyzing sounds recorded in isolation.

In contexts related to digital audio production, however, the most common convention is to assign $-1.0$ to the lowest air pressure and $+1.0$ to the highest air pressure which the audio device in question can handle. By audio device, we mean either a microphone which records sound or a speaker which produces it. Such a convention is especially useful because if a sound causes air pressure to drop below an amplitude of $-1.0$ or to exceed an amplitude of $1.0$, it will have an audible effect when the recorded sound is played again - you will hear distortion.

The crucial thing to remember is that the actual pressure values behind the amplitudes are irrelevant, only the changes in the amplitude matter. Therefore, the way we perceive a sound is uniquely determined by the shape of its waveform.

Example: Different Waveforms $⟹$ Different Sounds

To see how sound is affected by the shape of a waveform, listen to the following examples.

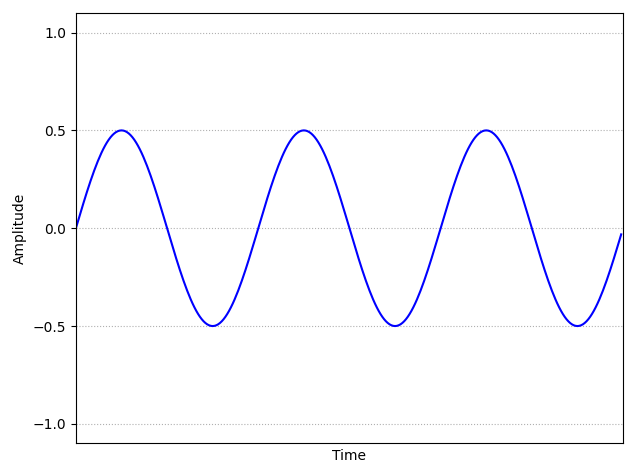
Sine Waveform:

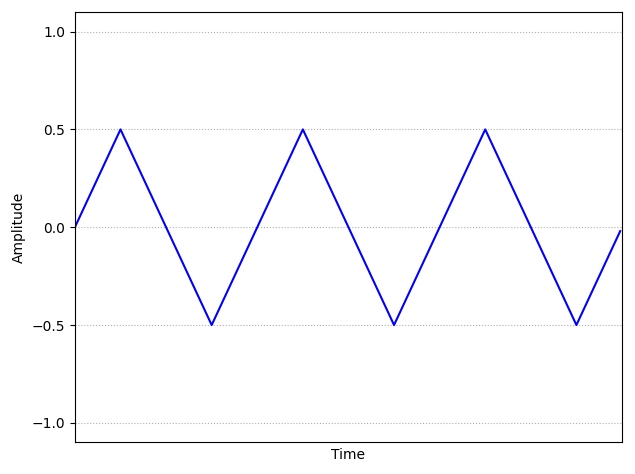
Triangle Waveform:

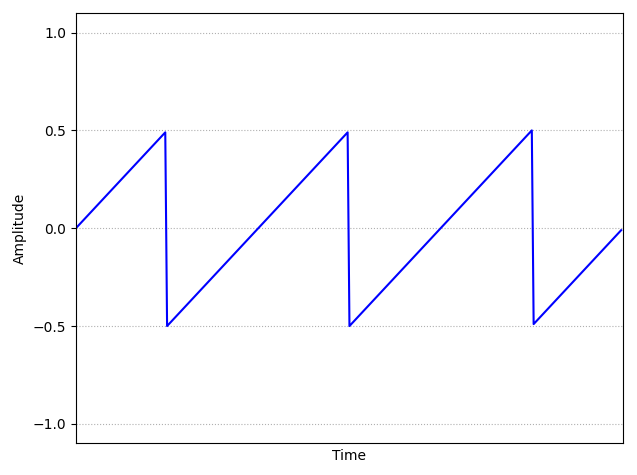
Sawtooth Waveform:

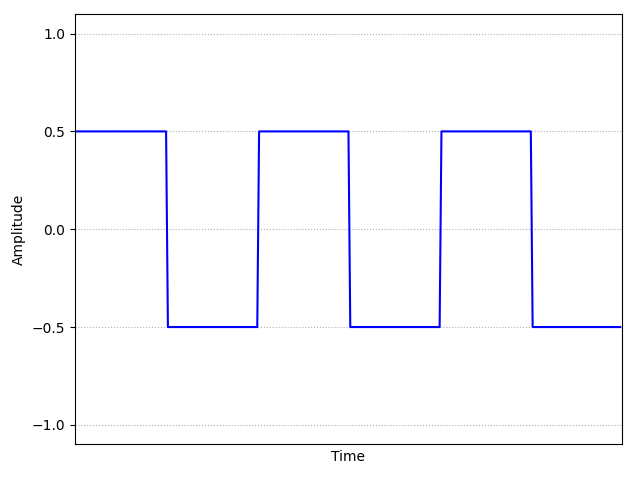
Square Waveform:

Note: Realistic Waveforms

In practice, the waveforms of actual, physical sounds have much more complex shapes than the simplified illustration above and look more like this:

However, if you zoom in close enough, you will see that it is ultimately the same thing as before.

Superposition

Sounds have one crucial property - they obey the superposition principle. If multiple sounds are playing at the same time, what we perceive is a single sound whose waveform is the combination of the waveforms of all the sounds playing.

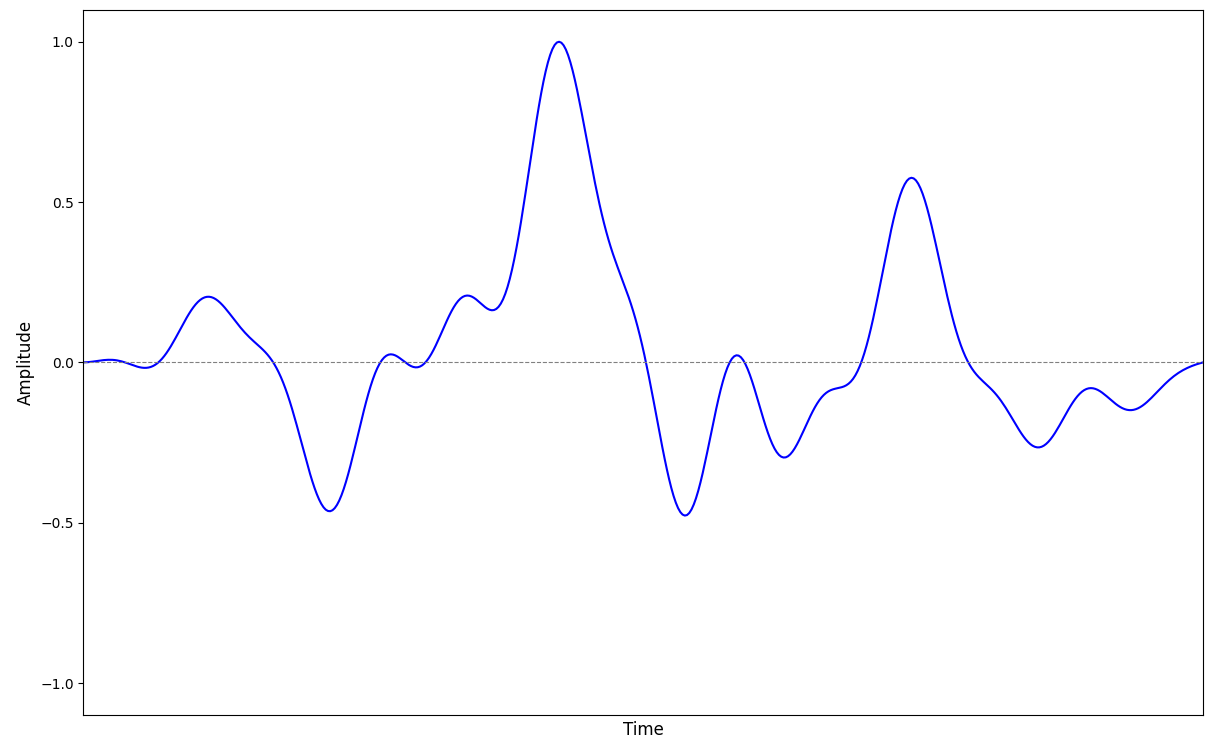
Consider two separate sounds $S_1$ and $S_2$. Let us denote by $S_1(t)$ the amplitude of $S_1$‘s waveform at time $t$ seconds after $S_1$ starts playing. Therefore, $S_1(2.5)$ would denote the amplitude of $S_1$‘s waveform $2.5$ seconds after $S_1$ starts playing. By analogy, $S_2(t)$ denotes the amplitude of $S_2$‘s waveform at time $t$ seconds after $S_2$ starts playing.

What we perceive is a sound $S$. Just as before, we shall use $S(t)$ to denote the amplitude of $S$‘s waveform at time $t$ seconds after $S$ starts playing. The superposition principle tells us that $S(t)$ is always the sum of $S_1(t)$ and $S_2(t)$:

$$S(t)=S_1(t)+S_2(t)$$

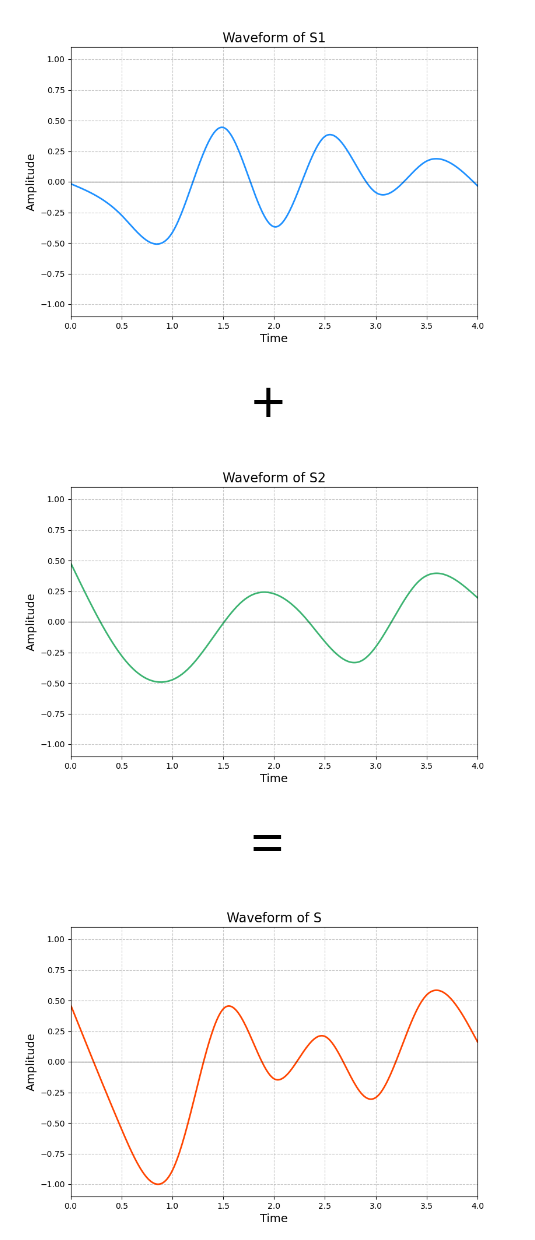
Sometimes, superposition is also called interference, of which there are two types:

• Constructive interference occurs whenever the amplitudes $S_1(t)$ and $S_2(t)$ have the same sign, i.e. they are both positive or both negative. When waveforms interfere constructively, the resultant amplitude $S(t)$ is further away from $0.0$. Examples of constructive interference in the above example can be found close to $t=1.0$ and $t=3.5$. Around $t=1.0$, the sounds $S_1$ and $S_2$ interfere constructively such that the amplitude of $S$ there is more negative than both the amplitudes of $S_1$ and $S_2$. Around $t=3.5$, the sounds interfere constructively such that the amplitude of $S$ there is more positive than both the amplitudes of $S_1$ and $S_2$.
• Destructive interference occurs whenever the amplitudes $S_1(t)$ and $S_2(t)$ have different algebraic signs, i.e. one is positive and the other is negative. When waveforms interfere destructively, the resultant amplitude $S(t)$ becomes closer to $0.0$. An example of destructive interference in the above example can be found close to $t=2.0$. The amplitude of $S_1$ there is negative while the amplitude of $S_2$ is positive. As a result, the amplitude of $S$ there is closer to $0.0$ than it would have been otherwise.

Tip: Noise Cancellation

Destructive interference is the principle which underpins noise cancellation. Noise-cancelling headphones are equipped with a tiny microphone on the outside. As external sounds pass through this microphone, they are recorded and analyzed by the headphones. The speakers inside the headphones then produce a sound whose waveform is designed to destructively interfere with the waveform of the external sound. This all happens so fast that the noise is cancelled before reaching your ears and so you do not hear it.