Double Integrals

Double Riemann Sums

Definition: Double Riemann Sum

Let $f:R\to \mathbb{R}$ be a Real Scalar Field over some rectangle $R=[a;b]\times [c;d]\subset {\mathbb{R}}^2$.

1. Subdivide the interval $[a;b]$ into $m$ intervals $[x_{i-1};x_i]$ of length $\Delta x=\frac{b-a}{m}$.

2. Subdivide the interval $[c;d]$ into $n$ intervals $[y_{i-1};y_i]$ of length $\Delta x=\frac{d-c}{n}$.

3. These subdivision result in smaller rectangles $R_{ij}=\{(x,y)\mid x_{i-1}\le x\le x_i,y_{j-1}\le y\le y_j\},$ each with area $\Delta A=\Delta x\Delta y$.

• For every choice of $(x_{ij}^{\ast },y_{ij}^{\ast })\in R_{ij}$ we get a double Riemann sum of $f$ over $R$.

$$\sum _{i=1}^m\sum _{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\Delta A$$

Double Integrals

Definition: Double Integral of a Real Scalar Field over a Rectangle

Let $f:R\to \mathbb{R}$ be a Real Scalar Field over some rectangle $R=[a;b]\times [c;d]\subset {\mathbb{R}}^2$.

The double integral of $f$ over $R$ is the limit of all of its double Riemann sums, if it exists and is the same for all of them.

$$\underset{m,n\to \infty }{\lim }\sum _{i=1}^m\sum _{j=1}^{n}f(x_{ij}^{\ast },y_{ij}^{\ast })\Delta A$$

NOTATION

$$\underset{R}{\iint }f\mathrm{dR}\underset{R}{\iint }f\mathrm{dA}\underset{R}{\iint }f(x,y)\mathrm{dA}$$

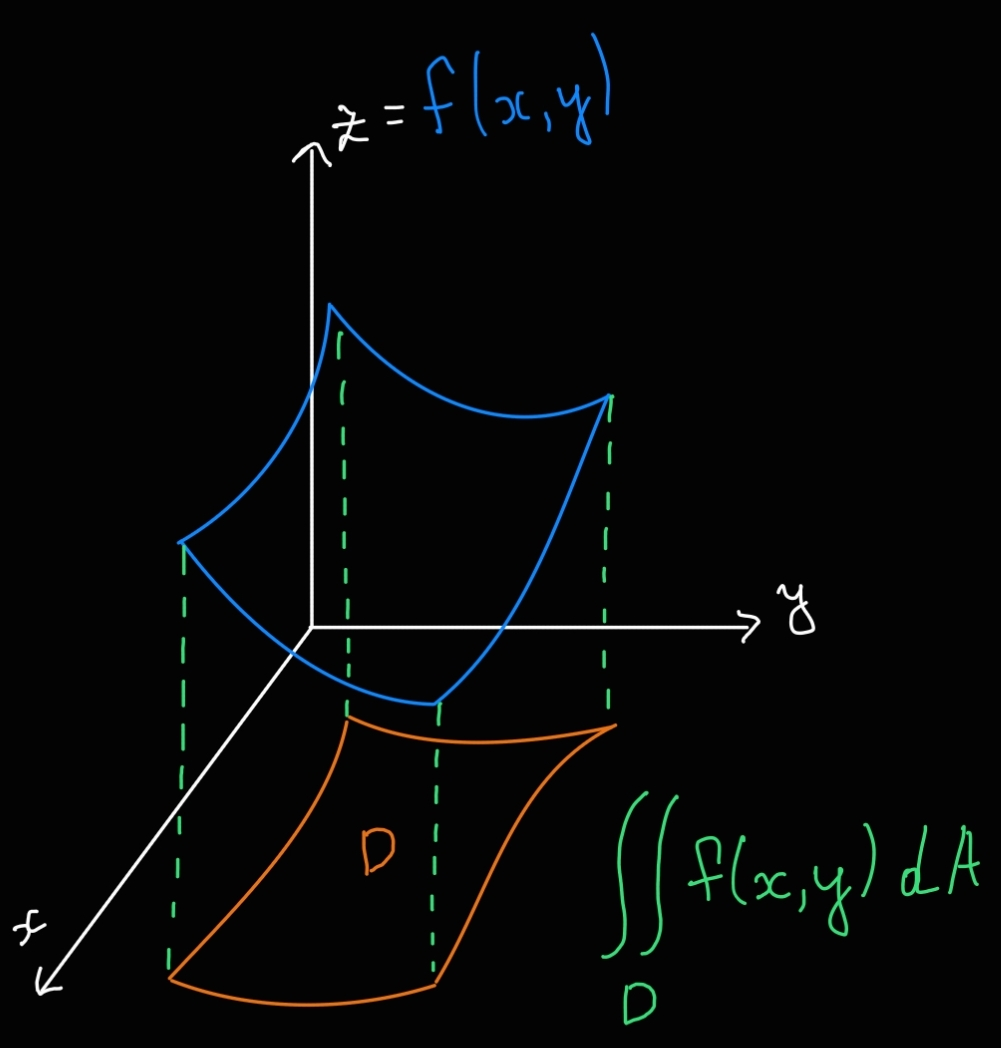
Definition: Double Integral of a Real Scalar Field over an Arbitrary Region

Let $f:D\subset {\mathbb{R}}^n\to \mathbb{R}$ be a Real Scalar Field.

The double integral of $f$ over $D$ is the double integral

$$\underset{R}{\iint }\mathcal{F}\mathrm{dR},$$

where $R\subset {\mathbb{R}}^2$ is any rectangle which completely contains $D$ and

$$\mathcal{F}(x,y)=\{\begin{array}{l}f(x,y),\text{if }(x,y)\in D\\ 0,\text{ if }(x,y)\in R\setminus D\end{array}$$

NOTATION

$$\underset{D}{\iint }f\mathrm{dD}\underset{D}{\iint }f\mathrm{dA}\underset{D}{\iint }f(x,y)\mathrm{dA}$$

Intuition: Geometric Meaning of the Double Intgeral

The double integral of $f$ over $D$ is the signed volume between the graph of $f$ and $D$.

Properties

Theorem: Linearity of the Double Integral

Let $f,g:D\to \mathbb{R}$ be real scalar fields over a general region $D\subset {\mathbb{R}}^2$.

The double integral is linear - for all $\lambda ,\mu \in \mathbb{R}$:

$$\underset{D}{\iint }\lambda f(x,y)+\mu g(x,y)\mathrm{dA}=\lambda \underset{D}{\iint }f(x,y)\mathrm{dA}+\mu \underset{D}{\iint }g(x,y)\mathrm{dA}$$

PROOF

TODO

Theorem: Double Integrals via Iterated Integrals

Let $f:\mathcal{D}\subseteq {\mathbb{R}}^2\to \mathbb{R}$ be a Real Scalar Field.

If $f$ is continuous and $\mathcal{D}$ can be expressed as $D=\left\{\left[\begin{array}{c}x\\ y\end{array}\right]\mid a\le x\le b,l(x)\le y\le u(x)\right\}$, where $l$ and $u$ are continuous real functions, then the double integral of $f$ over $\mathcal{D}$ can be calculated via iterated Parametric Integrals:

$$\underset{\mathcal{D}}{\iint }f\mathrm{dD}={\int }_a^b{\int }_{l(x)}^{u(x)}f(x,y)\mathrm{dy}\mathrm{dx}$$

If $f$ is continuous and $\mathcal{D}$ can be expressed as $\mathcal{D}=\left\{\left[\begin{array}{c}x\\ y\end{array}\right]\mid l(y)\le x\le u(y),a\le y\le b\right\}$, where $l$ and $u$ are continuous real functions, then the double integral of $f$ over $\mathcal{D}$ can be calculated via iterated Parametric Integrals:

$$\underset{\mathcal{D}}{\iint }f\mathrm{dD}={\int }_a^b{\int }_{l(y)}^{u(y)}f(x,y)\mathrm{dx}\mathrm{dy}$$

PROOF

TODO

Theorem: Region Decomposition

Let $f:\mathcal{D}\subset {\mathbb{R}}^2\to \mathbb{R}$ be a Real Scalar Field.

If $D$ can be represented as a union disjoint $\mathcal{D}={\mathcal{D}}_1\cup \cdots \cup {\mathcal{D}}_n$ of finitely many disjoint Sets, then the double integral of $f$ over $\mathcal{D}$ is the sum of the double integral of $f$ over ${\mathcal{D}}_1,\dots ,{\mathcal{D}}_n$:

$$\underset{\mathcal{D}}{\iint }f\mathrm{dD}=\underset{{\mathcal{D}}_1}{\iint }\mathrm{d}{\mathcal{D}}_1+\cdots +\underset{{\mathcal{D}}_n}{\iint }f\mathrm{d}{\mathcal{D}}_n$$

PROOF

TODO