Lebesgue Integration

Introduction

The notion of integration as the area under a curve or the volume under a surface can be generalized to real-valued functions $f:\mathcal{D}\subseteq X\to \mathbb{R}$, provided that we have some notion of assigning a size to the subsets of $X$, i.e. we have a measure on $X$.

This generalization is usually phrased explicitly for real functions $f:\mathcal{D}\subseteq \mathbb{R}\to \mathbb{R}$, but the exact same terminology is used with real-valued functions $f:\mathcal{D}\subseteq X\to \mathbb{R}$. It is thus useful to use real functions as a concrete example to provide motivation for the definitions, while still keeping in mind that the definitions also cover the more general case of real-valued functions as well.

Lebesgue Measure

Definition: Length of an Interval

Let $I$ be an interval of $\mathbb{R}$.

The length of $I$ is an extended real number defined as:

• $b-a$ if $I$ has one of the forms $[a;b]$, $(a;b)$, $[a;b)$ or $(a;b]$, where $a,b\in \mathbb{R}$;

• $\infty$ if $I$ has one of the forms $[a;\infty )$, $(a;\infty )$, $(-\infty ;b]$, $(-\infty ;b)$ or $(-\infty ;+\infty )$, where $a,b\in \mathbb{R}$.

NOTATION

$$l(I)$$

Definition: Generalized Volume of a Cuboid

Let $C$ be an open cuboid in the Euclidean space ${\mathbb{R}}^n$ with sides $I_1,\dots ,I_n$.

The volume of $C$ is the product of the lengths of $I_1,\dots ,I_n$:

$$\prod _{k=1}^{n}l(I_k)$$

NOTATION

$$\mathrm{vol}(C)$$

Theorem: Lebesgue Outer Measure

The function ${\lambda }^{\ast }:\mathcal{P}({\mathbb{R}}^n)\to \overline{\mathbb{R}}$ from the powerset of the Euclidean space ${\mathbb{R}}^n$ to the extended real numbers $\overline{\mathbb{R}}$ which is defined for each $E\subseteq {\mathbb{R}}^n$ as the infimum of the total volumes of all sequences $(C_k{)}_{k\in \mathbb{N}}$ of open cuboids which cover $E$, i.e.

$${\lambda }^{\ast }(E)\stackrel{\text{def}}{=}\inf \left\{\sum _{k=1}^{\infty }\mathrm{vol}(C_k):(C_k{)}_{k\in \mathbb{N}}\text{ is a sequence of open cuboids and }E\subseteq \bigcup _{k=1}^{\infty }{C}_k\right\},$$

is an outer measure on ${\mathbb{R}}^n$.

PROOF

TODO

Definition: Lebesgue Outer Measure

We call ${\lambda }^{\ast }$ the Lebesgue outer measure on ${\mathbb{R}}^n$.

Definition: Lebesgue Measure

Let ${\lambda }^{\ast }$ be the Lebesgue outer measure on the Euclidean space ${\mathbb{R}}^n$ and let $\Sigma$ be the collection of all ${\lambda }^{\ast }$-measurable sets.

The Lebesgue measure on ${\mathbb{R}}^n$ is the measure ${\lambda }^n:\Sigma \to \overline{\mathbb{R}}$ generated by Carathéodory’s extension theorem using the Lebesgue outer measure ${\lambda }^{\ast }$.

Definition: Lebesgue-Measurability

A subset $S\subseteq {\mathbb{R}}^n$ is Lebesgue-measurable if $S\in \Sigma$.

The Lebesgue measure is necessary for defining integration for real-valued functions $f:\mathcal{D}\subseteq X\to \mathbb{R}$ but $\mathcal{D}$ itself may have nothing to do with ${\mathbb{R}}^n$ or $\mathbb{R}$.

Lebesgue Integrals

Consider a subset $S\subseteq \mathbb{R}$ and its indicator function $1_S:\mathbb{R}\to \mathbb{R}$. The graph of $1_S$ would resemble the following, since $1_S(x)=1$ if $x\in S$ and $1_S(x)=0$ otherwise:

The area under the graph of $1_S$ is just the sum of the shaded areas, all of which have a height of $1$. The area of each of these is given by $1\cdot \mu (S_i)$, where $\mu (S_i)$ is the size (length) of each blue piece. Therefore, the area under the graph of $1_S$ is ${\sum }_{i}1\cdot \mu (S_i)=1\cdot {\sum }_i\mu (S_i)={\sum }_i\mu (S_i)$. However, the sum ${\sum }_i\mu (S_i)$ of the sizes of the blue pieces $S_i$ is just equal to the size $\mu (S)$ of $S$. Thus we define the integral of $1_S$ in the following way.

Definition: Lebesgue Integral of Indicator Functions

Let $(X,\Sigma ,\mu )$ be a measure space, let $S\subseteq X$ be measurable and let $1_S:X\to \mathbb{R}$ be the indicator function of $S$.

The (Lebesgue) integral of $1_S$ with respect to $\mu$ is the measure of $S$:

$$\int 1_S\mathrm{d\mu }\stackrel{\text{def}}{=}\mu (S)$$

We now extend this definition to functions which can be built from finitely many indicator functions.

Definition: Simple Function

Let $(X,\Sigma ,\mu )$ be a measure space and let $\varphi :\mathcal{D}\subseteq X\to {\mathbb{R}}_{\ge 0}$ be a real-valued function.

We say that $\varphi$ is a simple function if $\mathcal{D}$ can be represented as the union of a finite collection disjoint measurable sets $\mathcal{D}={\mathcal{D}}_1\cup \cdots \cup {\mathcal{D}}_n$ and there exist $n$ real numbers $c_1,\dots ,c_n\ge 0$ such that

$$\varphi (x)=\sum _{i=1}^n{c}_i{1}_{{\mathcal{D}}_i}(x)\forall x\in \mathcal{D},$$

where $1_{{\mathcal{D}}_i}$ is the indicator function of ${\mathcal{D}}_i$.

Consider a simple real function $\varphi :\mathcal{D}\subseteq \mathbb{R}\to \mathbb{R}$.

The are under its graph is just the sum of the shaded areas. All shaded areas with a blue bottom have a height of $c_1$ and all shaded areas with a green bottom have a height of $c_2$. Applying the same reasoning as we did with indicator functions, the total shaded area with a blue bottom is $c_1\cdot \mu ({\mathcal{D}}_1)$. Similarly, the total shaded area with a green bottom is $c_2\cdot \mu ({\mathcal{D}}_2)$. The area under the graph of $\varphi$ is then given by summing these two areas: $c_1\cdot \mu ({\mathcal{D}}_1)+c_2\cdot \mu ({\mathcal{D}}_2)$. More generally, when $\mathcal{D}$ must be decomposed into $n$ subsets $\mathcal{D}={\mathcal{D}}_1\cup \cdots \cup {\mathcal{D}}_n$, the total area is given by ${\sum }_{i=1}^n{c}_i\cdot \mu ({\mathcal{D}}_i)$.

Definition: Lebesgue Integral of Simple Functions

Let $(X,\Sigma ,\mu )$ be a measure space and let $\varphi :\mathcal{D}\subseteq X\to {\mathbb{R}}_{\ge 0}$ be a real-valued function such that $\mathcal{D}$ can be represented as the union of a finite collection disjoint measurable sets $\mathcal{D}={\mathcal{D}}_1\cup \cdots \cup {\mathcal{D}}_n$ and there exist $n$ real numbers $c_1,\dots ,c_n\ge 0$ with

$$\varphi (x)=\sum _{i=1}^n{c}_i{1}_{{\mathcal{D}}_i}(x)\forall x\in \mathcal{D}.$$

The (Lebesgue) integral of $\varphi$ with respect to $\mu$ is defined using the measures of ${\mathcal{D}}_i$ as

$$\int \varphi \mathrm{d\mu }\stackrel{\text{def}}{=}\sum _{i=1}^n{c}_i\mu ({\mathcal{D}}_i),$$

with the convention $0\cdot \infty =0$.

This definition can be extended to non-negative real-valued functions. Consider a real function $f:\mathcal{D}\subseteq \mathbb{R}\to {\mathbb{R}}_{\ge 0}$. We can approximate $f$ using a simple function. Choose $n\in \mathbb{N}$ values $c_1,\dots ,c_n\in f(\mathcal{D})$ from the range of $f$ and let ${\mathcal{D}}_i=\{x\in \mathcal{D}\mid f(x)\ge c_i\}$. Define $\varphi :\mathcal{D}\subseteq \mathbb{R}\to {\mathbb{R}}_{\ge 0}$ in the following way:

$$\varphi (x)\stackrel{\text{def}}{=}\{\begin{array}{l}{c}_1\text{if }x\in {\mathcal{D}}_1\\ ⋮\\ c_n\text{if }x\in {\mathcal{D}}_n\end{array}$$

We see $\varphi$ is a simple function

$$\varphi (x)=\sum _{i=1}^n{c}_i{1}_{{\mathcal{D}}_i}(x),$$

since $1_{{\mathcal{D}}_j}(x)$ gives $1$ only when $x\in {\mathcal{D}}_j$ and gives $0$ otherwise. Therefore, $\varphi (x)=c_j$ if and only if $x\in {\mathcal{D}}_j$. Of course, if we choose only a few values $c_1,\cdots ,c_n$, then $\varphi$ will be a pretty bad approximation of $f$. However, as we increase the number of values $n$, $\varphi$ becomes a better and better approximation. This is illustrated in the following animation:

Lines with the same color correspond to the same value $c_j$ and ${\mathcal{D}}_j$ is the part of the of $\mathbb{R}$ which lies directly below the lines corresponding to $c_j$.

The more closely $\varphi$ approximates $f$, the more the area under the graph of $\varphi$ resembles the area under the graph of $f$:

This notion of $\varphi$ approximating $f$ can be defined and proven rigorously via function sequences and their limits but that is unnecessary. Notice that $0\le \varphi (x)\le f(x)$ for all $x\in \mathcal{D}$. Consider now the set $S$ of the integrals of all simple functions $s:\mathcal{D}\subseteq \mathbb{R}\to \mathbb{R}$ such that $0\le s(x)\le f(x)$ for all $x\in \mathcal{D}$. Since these simple functions are always less than or equal to $f$, the areas under their graphs must be less than or equal to the area under the graph of $f$. The supremum of $S$, i.e. the largest of these areas, is thus as close as one could get to the area under the graph of $f$. Moreover, it can be proven that this is equal to the integral of $\varphi$ as $\varphi$ becomes a better approximation of $f$.

Definition: Integration of Non-Negative Functions

Let $(X,\Sigma ,\mu )$ be a measure space and let $f:\mathcal{D}\to {\mathbb{R}}_{\ge 0}$ be a measurable (in the sense of the Lebesgue measure) real-valued function on a measurable subset $\mathcal{D}\subseteq X$.

The integral of $f$ is the supremum of the set of all integrals of simple functions $s$ such that $0\le s\le f$:

$$\int f\mathrm{d\mu }\stackrel{\text{def}}{=}\sup \left\{\int s\mathrm{ds}\mid s\text{ is simple and }0\le s\le f\right\}$$

Extending the above definition to real-valued functions which can also take on negative values is fairly easy. Consider a real function $f:\mathcal{D}\subseteq \mathbb{R}\to \mathbb{R}$. Essentially, we split $f$ into a negative and a non-negative part. We take the area between the horizontal axis and the graph of $f$‘s non-negative part of $f$ and subtract from it the area between the horizontal axis and the graph of $f$‘s negative part. This gives us a notion of the signed area between the horizontal axis and the graph of $f$ and thus yields a good definition for the integral of $f$.

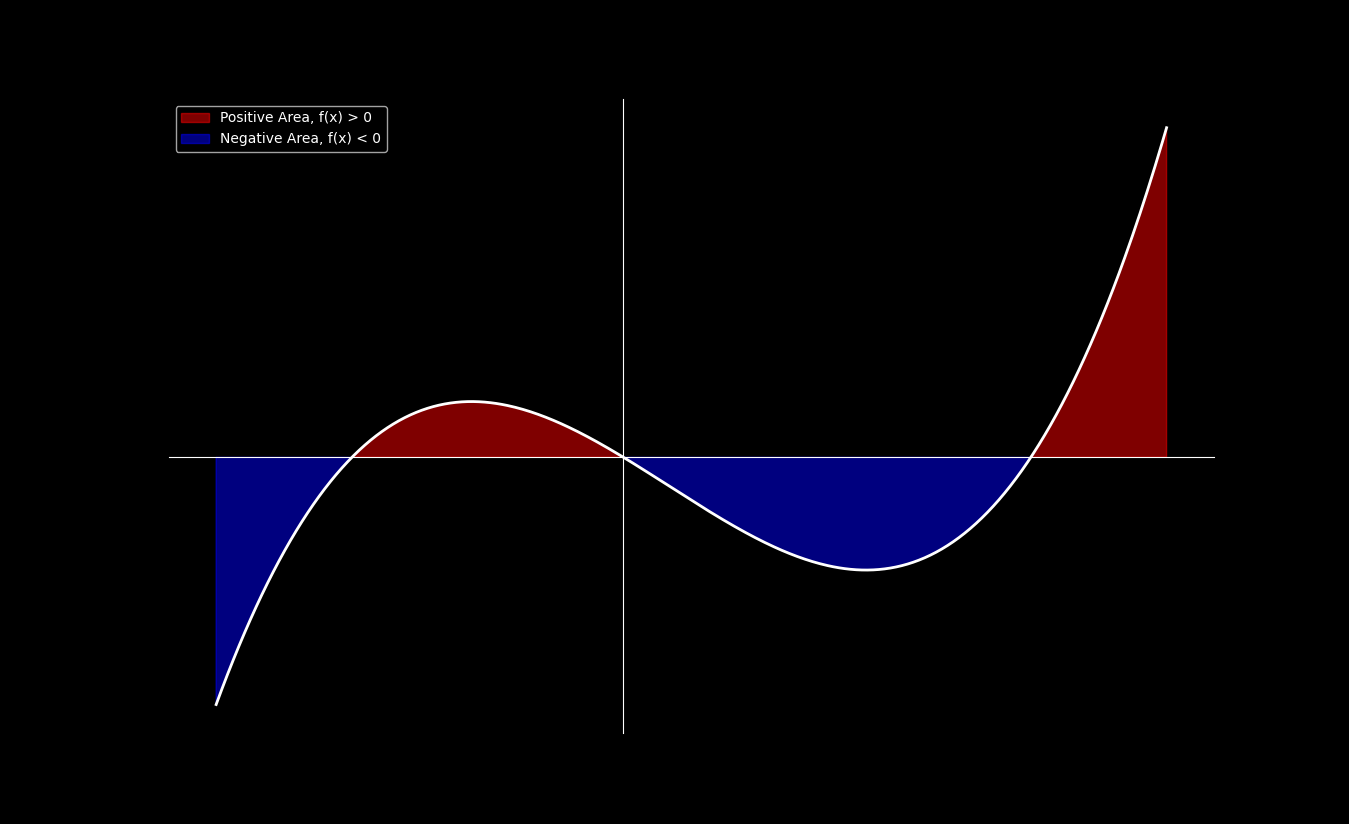
Definition: Integration of General Functions

Let $(X,\Sigma ,\mu )$ be a measure space, let $f:\mathcal{D}\to \mathbb{R}$ be a measurable (in the sense of the Lebesgue measure) real-valued function on a measurable subset $\mathcal{D}\subseteq X$ and let $f^{-}=\max (-f,0)$ and $f^{+}=\max (f,0)$.

The (Lebesgue) integral of $f$ with respect to $\mu$ is defined using the integrals of $f^{-}$ and $f^{+}$ as

$$\int f\mathrm{d\mu }\stackrel{\text{def}}{=}\int f^{+}\mathrm{d\mu }-\int f^{-}\mathrm{d\mu },$$

provided that at least one of $\int f^{+}\mathrm{d\mu }$ or $\int f^{-}\mathrm{d\mu }$ is finite (in order to avoid $\infty -\infty$).

We say that $f$ is $\mu$-integrable if its integral is finite.

Definition: Integrating on a Subset

Let $S$ be a measurable subset $S\subseteq X$.

The (Lebesgue) integral of $f$ over $S$ with respect to $\mu$ is the integral

$${\int }_{S}f\mathrm{d\mu }\stackrel{\text{def}}{=}\int f\cdot 1_S\mathrm{d\mu },$$

where $1_S$ is the indicator function of $S$.

We say that $f$ is $\mu$-integrable on $S$ if its integral on $S$ is finite.

Note: Lebesgue Integral with Respect to the Lebesgue Measure

When $X$ is ${\mathbb{R}}^n$ (or $\mathbb{R}$) and $\mu$ is the Lebesgue measure on ${\mathbb{R}}^n$ (or $\mathbb{R}$), then we just say “Lebesgue integral” and omit “with respect to”. Similarly, we just say that $f$ is “Lebesgue-integrable”.

Theorem: Integrability Criterion

Let $(X,\Sigma ,\mu )$ be a measure space, let $f:\mathcal{D}\to \mathbb{R}$ be a measurable (in the sense of the Lebesgue measure) real-valued function on a measurable subset $\mathcal{D}\subseteq X$ and let $S$ be a measurable subset $S\subseteq X$.

The function $f$ is $\mu$-integrable on $S$ if and only if the integral of its absolute value is $\mu$-integrable on $S$:

$${\int }_{S}f\mathrm{d\mu }<\infty ⟺{\int }_S|f|\mathrm{d\mu }<\infty$$

PROOF

TODO